データの取得,正規分布,T検定
実験データ取得、解析を必要とする学生、企業技術者の皆様。
測定データがばらついてしまって、サンプル間の差があるかどうか判断に困ったことはないだろうか?
この記事では、そんな時に役立つ『T検定』がどのようなものかをご紹介します。
また、エクセルでの計算方法もご紹介。
1.データの取得とは?
2.正規分布とは?
3.標準偏差とは?
4.T検定って何?
5.エクセルでやってみよう!!
1.データの取得とは?
まず、データを取得するとは、大きな集団(母集団)の中からサンプリング(標本抽出)を行っているということです。採取した標本データから平均値やバラツキなどの情報を得ることができ、そこから母集団の情報を推定できます。
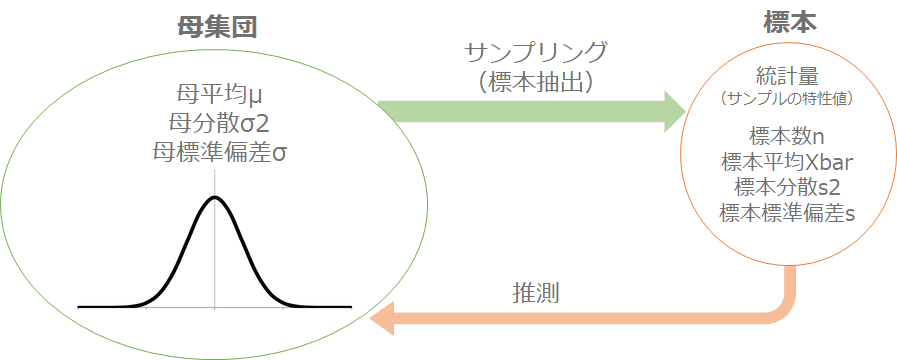
✔データ取得は母集団の情報を知るために実施している。
2.正規分布とは?
採取したデータは必ず分布を持ちます。例えば正規分布が有名ですね。全てではありませんが多くのデータが正規分布に従うとされています。例えば日本人の伸長、ある学校のテストの点数などがそうです。図で表すとこのような感じになります。一度は見かけたことがありますかね?
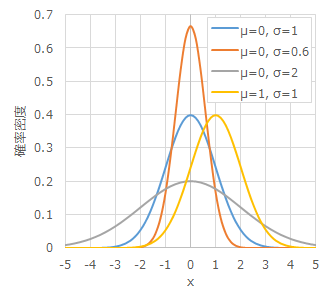
縦軸は確率密度といい、範囲を指定して積分すると確率になります。要するにどの値になる可能性が高いかを表しているのですね。例えば平均値μ=0、標準偏差σ=0.6のグラフ(橙)を見てみると、xは最も0になる確率が高く、3以上になる確率はほとんどないことが分かります。正規分布は平均値を中心として左右対称であり、標準偏差で形が決まるのですが、上の図を見るとわかるとおり、標準偏差(バラツキ)が小さいほど鋭い形状(橙)となり、逆に大きいと緩やかな形状(灰色)となります。また、正規分布において平均値±3σの間にデータの99.7%が収まります。
✔左右対称である。
✔平均値μと標準偏差σで形が決まる。
σが小さい→狭い分布 σが大きい→広い分布
✔平均値±3σに99.7%が収まる。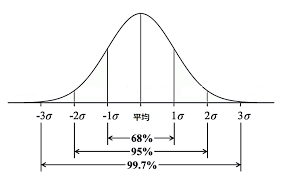
3.標準偏差とは?
標準偏差、言葉を聞いたことはあるでしょう。実際に実験データのバラツキの指標として使用している方も多いのではないでしょうか?今回は実際に標準偏差の式を見ながらその意味を考えてみたいと思います。
標準偏差を計算するためにはまず偏差平方和を計算する必要があります。

偏差平方和は「平均値とデータの差」を2乗し足し合わせたものなので、
「平均値からデータがどれだけずれているか」を表す統計量です。
続いて、偏差平方和をデータ数で割ったものが分散です。

平方和を標本数nで割っているのでデータ1つ分の平均値からのズレを表しています。ただし、2乗がかかっているので、平均値の単位とは異なっています。例えば身長cmの分散を計算した場合、分散の単位はcm2ですね。
最後に、分散の平方根をとることで標準偏差となります。

ここで標準偏差の単位は平均値と同じになるので(身長ならcm)、平均値と並べてデータのバラツキ具合を議論する場合には標準偏差を使うとよいのですね。
標準偏差のイメージがつきましたか?ここまで説明してきたものは「標本の標準偏差」です。例えば、10000個の母集団から100個の標本を抜き出したとすると、標本100個がどれくらいバラついているかを示しています。その標本から得られたバラツキから母集団のバラツキを推測することができます。つまり私たちが知りたい大元の10000個のデータのバラツキが標本の情報からわかってしまう訳です。
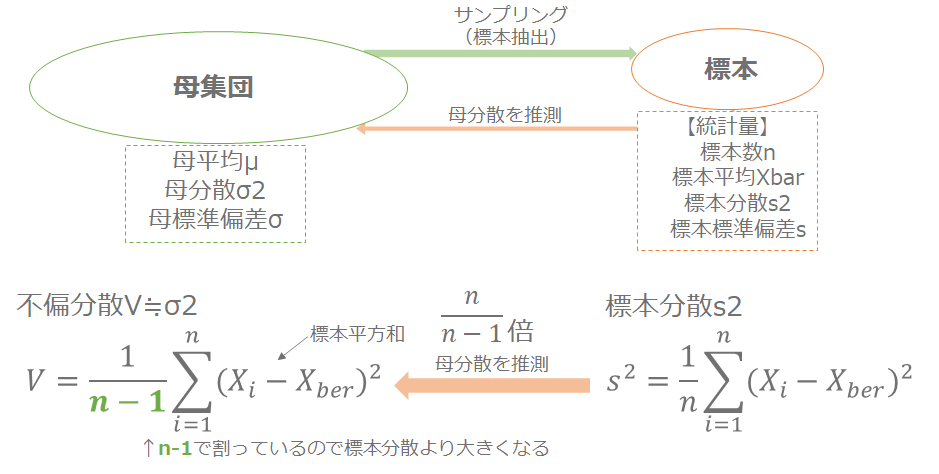
標本分散から推測される母集団の分散を不偏分散Vと呼びます。標本分散の場合は平方和を標本数nで割りますが、不偏分散の場合はn-1で割っています。なので母集団の分散は、標本分散より大きくなるということです。母分散が分かったので、母分散の平方根をとることで母集団の標準偏差を算出することができますね。基本的には、データを採取してきて母集団について議論したい場合は不偏分散(n-1で割った方)を使うのが良いでしょう。
4.T検定って何?
データをとっていて平均値Xと平均値Yで差があるかどうかを判定したいと思ったことはないですか?そんな時はT検定!!それぞれの平均値(xber,yber)、分散(s2)、標本数(m,n)を用いた検定統計量という数値を計算して平均値に差があるかを判定することができます。
T検定に使用する検定統計量であるt値は上記に示した通り何種類かあります。式も少しややこしいですね。それぞれについて簡単に説明しておきましょう。
①はXとYが対になっているようなときに使います。例えば、5人に薬を投与して効果があったかどうかを判定する場合、各人の投与前と投与後のデータを比較する必要があります。Aさんの投与前と投与後、Bさんの投与前と投与後のデータが対になっているということですね。このような場合①のt値を使用します。
②はXとYの分散が等しいとときに使う検定量です。これを使う場合は厳密にいえばXとYの分散が等しいかどうかを判定するF検定というものをあらかじめ実施する必要があります。
③はウェルチの検定と呼ばれ、XとYの分散が等しくなくても使える検定量です。
式をちょっと眺めてみてください。①②③いずれも2つの平均値の差(X-Y)を表す式になっていますね。なのでもしX=Yであればt値も0になるということです。
これらの検定統計量を使ってどのように差を判定するかはざっくりこんな感じです。
✔X=Yであるという仮説を立てる(帰無仮説)
✔実際のX、Yからサンプリングしてt値を計算する
✔t値がt分布の95%側に入るか5%側に入るか確認する。
☆T分布について☆
XとYからサンプリングしてt値を何度も計算すると、いろいろなt値が計算されるので、t値の分布ができます。それがt分布です。t値はX-Yが分子にあるので、X=Yと仮定した場合0になる確率が最も高く、0から離れるほど確率が小さくななり、t分布は0を中心とした左右対称の確率密度関数となります。下のt分布の図でいえば、X=Yのときt値は±2.26の間に95%が収まるはずです。
【T分布】
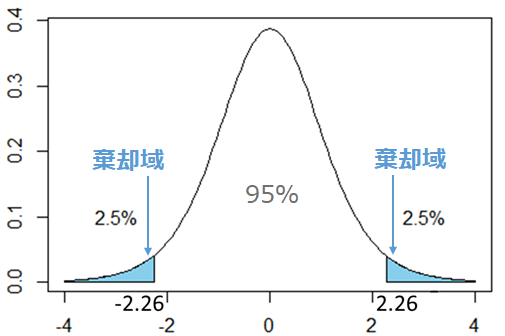
t分布は自由度(X標本数-1+Y標本数-1)によって形が変わってきますが、自由度がきまればt表から5%の境界となるtの値を読み取ることができます。また、エクセルで計算する場合、5%境界値以上のt値となるときの確率を表すP値を計算することができます。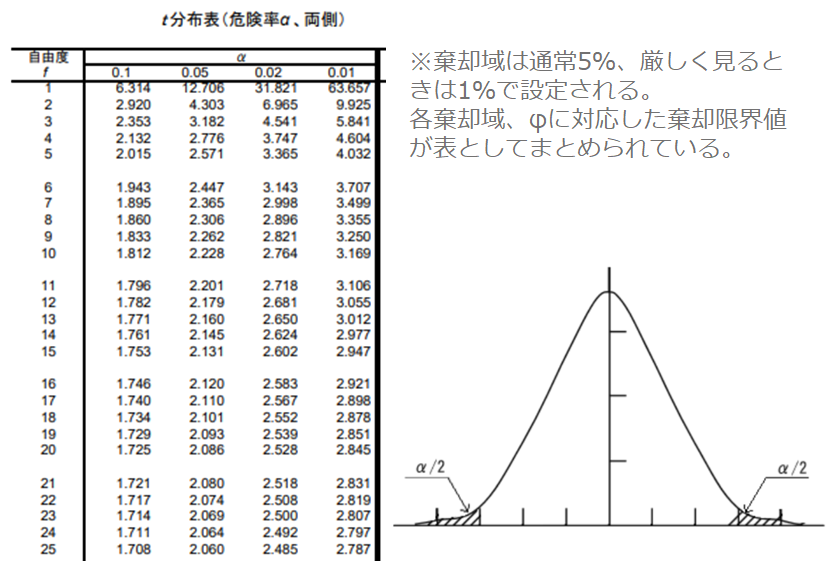
✔t値が5%側に含まれる場合、X=Yでは5%の確率でしか起こらないことを意味する
例えば、表から読み取った5%の境界t値より計算したt値が大きくなる場合やt値から計算したP値が0.05より小さい場合は、t値が5%の確率でしかt分布に含まれないことを意味する。
✔5%でしかおこらないので最初の仮説が正しくないと判断する
⇒帰無仮説を棄却する。
✔「X=Yではなく、X≠Yである」と判断する。
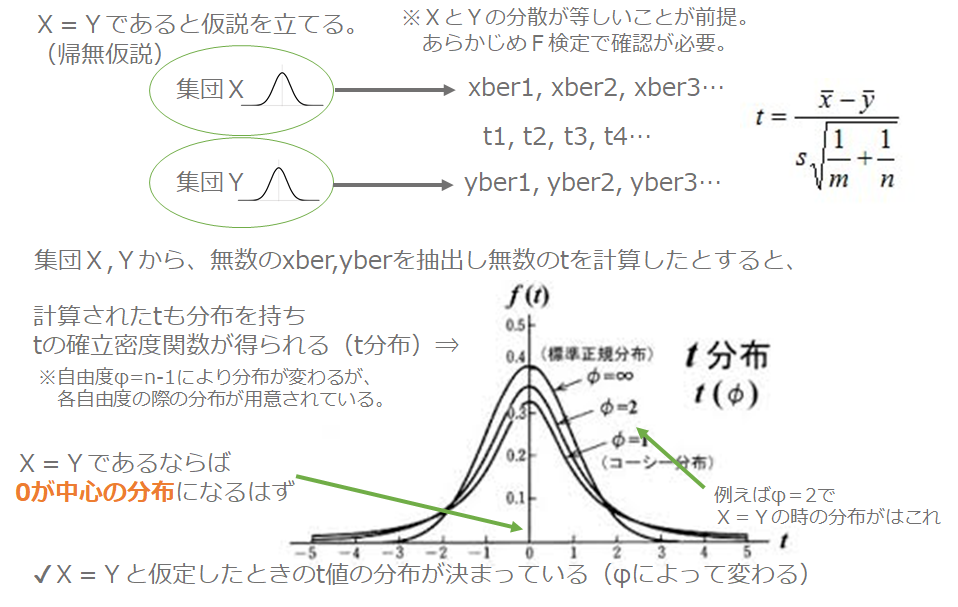
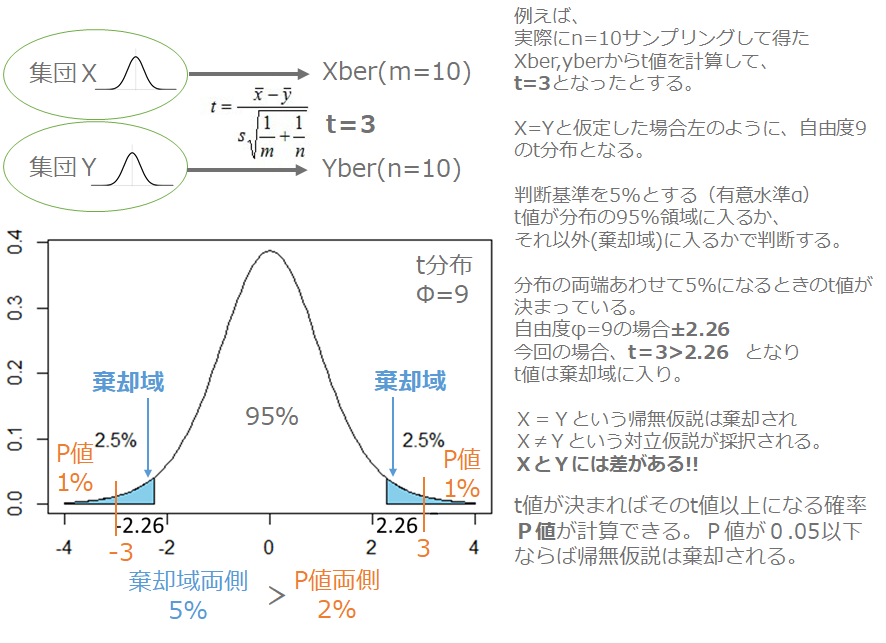
すこし分かりづらかったと思いますが、簡単にいうとX=Yと仮定したときのt値の分布が決まっていて、実際に計算した時のt値がその分布の中に含まれているかどうかをみているということですね~。t値がその分布に含まれるのなら仮説が正しいのでX=Y、もし分布に含まれにくいのであればX≠Yとなります。
5.エクセルでやってみよう!!
これまで説明した標準偏差やT検定はエクセルで簡単に計算できます。エクセル関数の一覧はこちら↓↓
| 関数 | |
| =STDEV.P(セル範囲) | 標本データの標準偏差 |
| =STDEV.S(セル範囲) | 標本から予測した母集団の標準偏差 |
| =STDEVA | =STDEV.S |
| =STDEVPA | =STDEV.P |
| =T.TEST(配列1, 配列2, 検定の指定, 検定の種類) | 配列1,2から計算したt値に対応するP値を算出。 |
| =F.TEST(配列1, 配列2) | 配列1,2のから計算したf値に対応するP値(両側)を算出。 |
標準偏差の関数は主に二つあり、標本データの標準偏差の計算には「STDEV.P」を使用します。母集団の標準偏差を計算したい場合は「STDEV.S」を使用します。基本的には母集団の標準偏差が必要な場合が多いですかね。他にも「STDEV」や「SRDEVPA」もありますが中身は「STDEV.S」「STDEV.P」と同じなのでいずれかを覚えておけばOKです。ちなみにSTDEVはstandard deviation(標準偏差)の略のようです。
【標準偏差_STDEVの実用例】
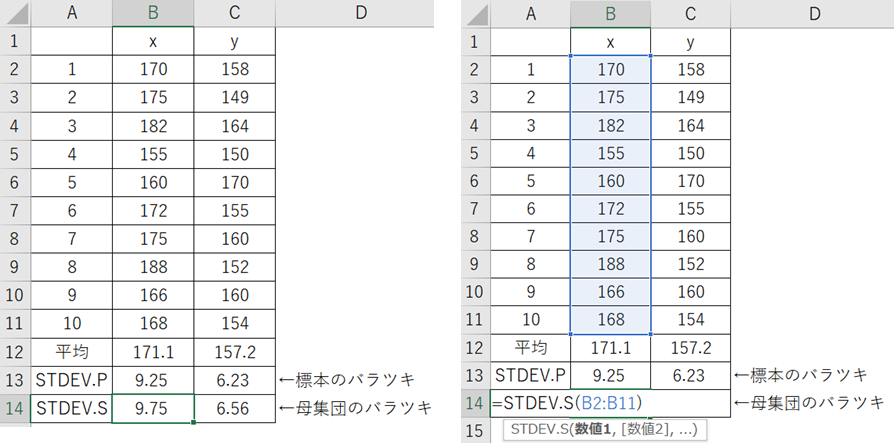
標準偏差の関数の使い方は簡単です。=STDEV.Sを打ち込んで標準偏差を計算したいデータの範囲を選ぶだけ!!
【F検定_F.TESTの実用例】
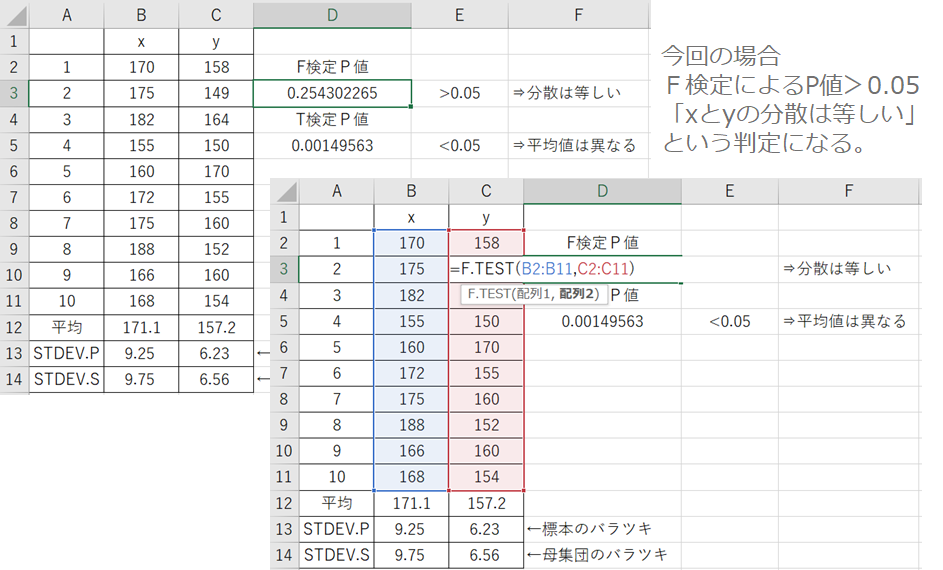
F検定はデータの分散に差があるかを調べるときに使います。上述した②の分散が等しいことを仮定したT検定を実施する前には確認のためF検定を実施するのが良いでしょう。=F.TESTと打ち込み、比較したいデータの範囲をそれぞれ選択するとF検定のP値を計算してくれます。このP値が0.05以下であればXとYの分散は等しくないということになります。上の図ではP値が0.25になっており0.05より大きいためXとYの分散は等しいという判定になります。
【T検定_T.TESTの実用例】
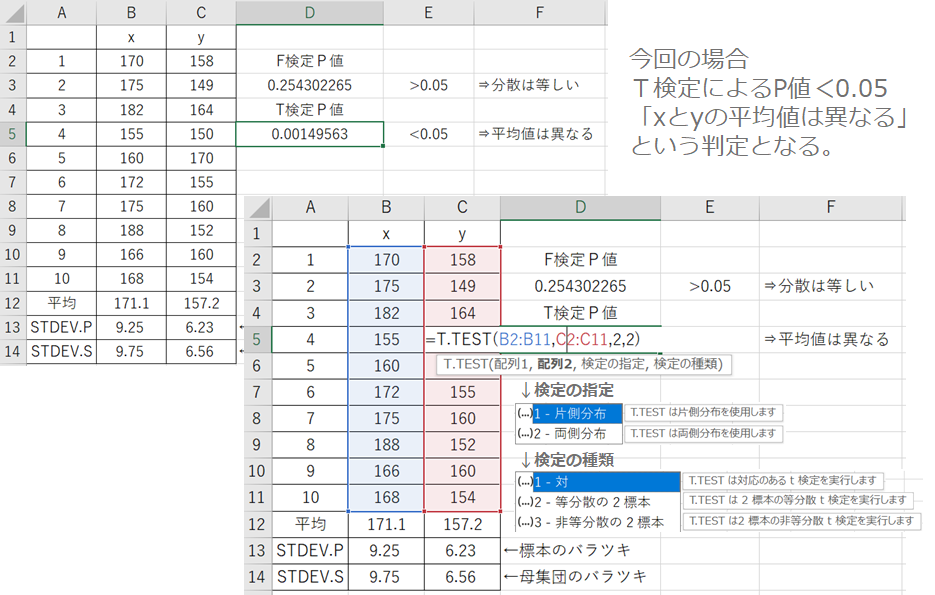
T検定では平均値に差があるかを調べるときに使うことができます。=T.TESTと入力し、比較したいデータの範囲をそれぞれ選択し、検定の指定と検定の種類を選ぶことでT検定のP値を計算してくれます。検定の指定は1_片側分布、2_両側分布となっており、X≠Yであるかを検定する場合には両側検定、X>Y or X<Yであるかを検定する場合は片側検定となります。単純に差があるかどうかを知りたい場合は2_両側分布を選びましょう。検定の種類は、上述した通りでデータが対になっているようなものであれば1、等分散を仮定した2標本を比較したい場合は2、非等分散の場合は3を入力してください。計算されたP値が0.05以下であればXとYの平均値は等しくないということになります。上の図ではP値が0.0015になっており0.05より小さいためXとYの平均値は異なるという判定です。
分析ツールを使う方法_T検定
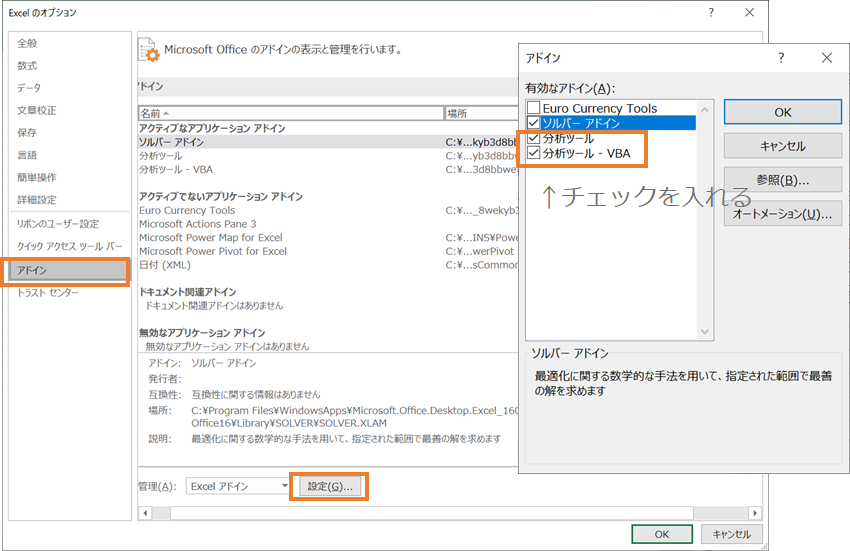
分析ツールを使ったやり方もあります。エクセルのデータタブを選択すると右端に「データ分析」があります。※出てきていない方は以下の【分析ツールが表示されていない方】へを参照下ください。
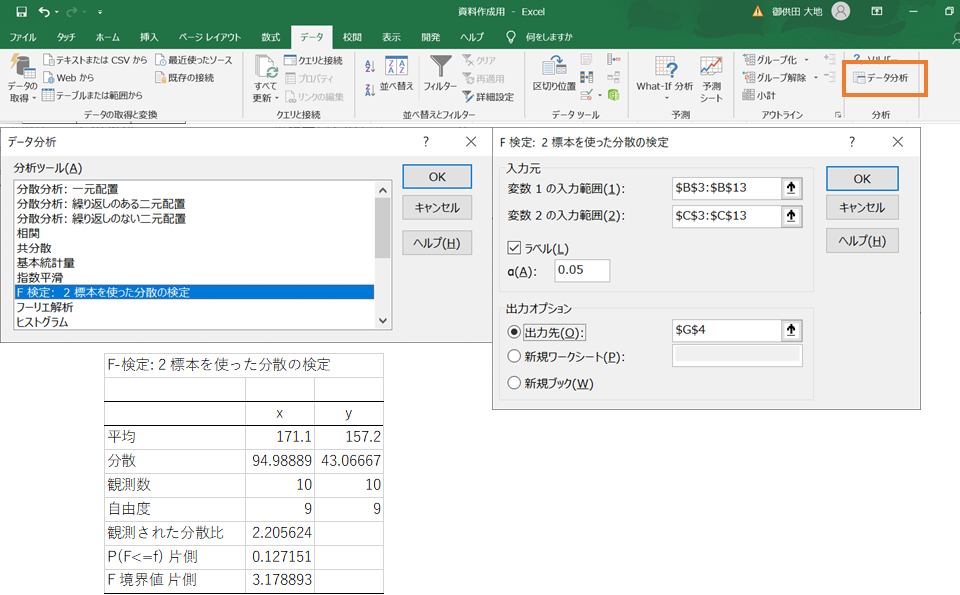
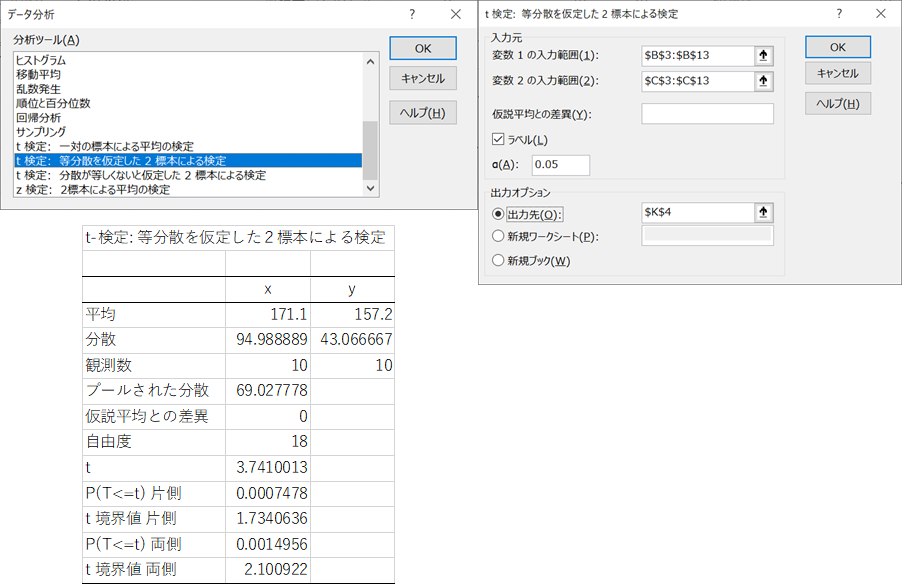
以下の操作をすることで各種統計量が算出されます。
「データ分析」⇒「F検定 or T検定」⇒変数1、変数2の範囲の設定⇒αの設定⇒出力先の設定⇒OK
データ名(この場合x、y)を選択範囲に入れた場合はラベルにチェックを入れてください。